동차 좌표계 (Homogeneous Coordinates)
기하 연산에서의 장점
1) 공통의 행렬 연산으로 구현할 수 있다.
2) 최종 행렬 하나로서 전체 변환을 적용한다.
3) 무한 지점의 좌표를 변환할 수 있다.

(1,2) 방향으로 무한히 멀리 있는 점을 표현할 수 있다.
vanishing point (소실점) and lines(소실선)
직선의 방정식을 이용해 영상을 좌표로 표현할 수 있다.

2D Translation

2D Rotation
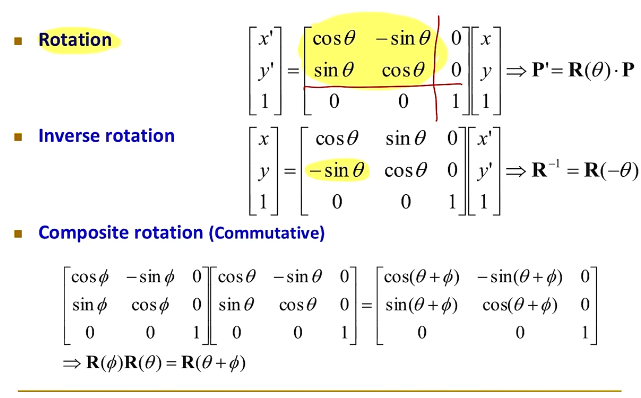
2D Scaling
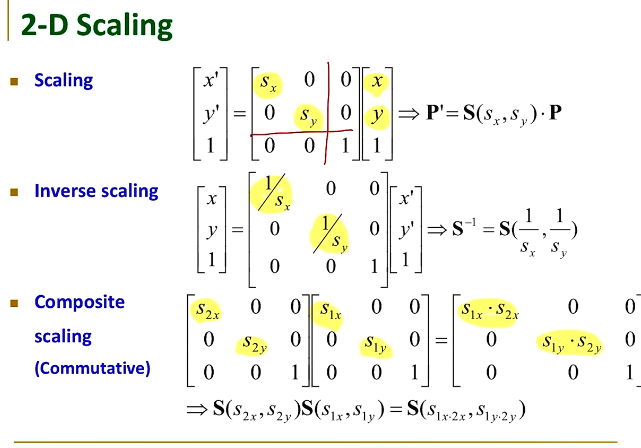
Rotation의 과정
1) Transation
2) Rotation
3) Translation

위와 같이 세 단계의 행렬 연산을 함축해 표현할 수 있다.
여기서 세타 값이 180이라면 특정 점에 대해 대칭으로 이동할 수 있다.
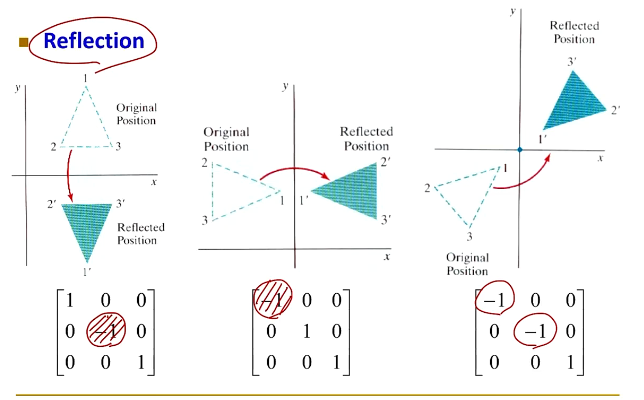
Reflection의 경우 아래와 같이 행렬 연산을 해주어서 아래, 옆, 대각선으로 Transformation을 수행한다.
추가적인 Transfrom에는 Affine과 Projective가 있다.
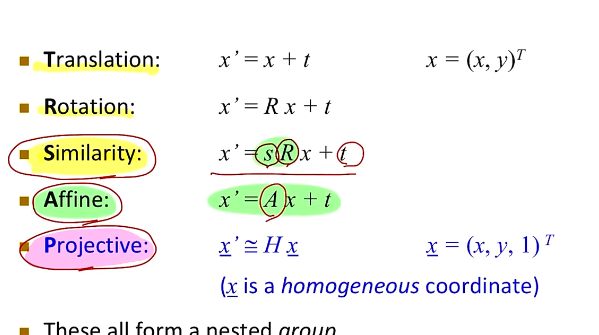
Projective Transformation은 주어진 영상에 대해서 각도도, 크기도 바뀌는 경우를 말한다.

3D Transformation에서는 동차 좌표계 특성에 맞게 layer를 하나 더 추가해서 구현할 수 있다.
'Major Study > Digital Image Processing' 카테고리의 다른 글
| Lecture 11. Image Stitching (Panorama) (1) | 2022.06.09 |
|---|---|
| Lecture9 : Local Feature Detection and Matching (0) | 2022.06.09 |
| Lecture8 : Clustering and Segmentation (군집화와 영역화) (0) | 2022.06.03 |
| 주파수 영역 필터링(Filtering in Frequency Domain) (0) | 2022.04.05 |
| C++을 이용한 선형 필터링(Linear Filtering ) 구현하기 (0) | 2022.03.31 |
