Local Features
image에서 patch 한 부분들 중 유사한 바운더리를 가지는 것을 Match해 Parnorama Stitching을 수행할 수 있다.
밝기가 바뀌는 Edge, Corner Point를 patch화해서 특징을 본다면 Matching Point를 찾아 1:1 대응이 가능
PipeLine : Detectionn, Description, Matching
기존 이미지에서 Similarity Tranfrom 을 한 경우, 특징점을 Normalize해서 Patch의 방향을 고정
즉 Normalize를 통해 방향과 크기를 확정한다.
vector 간의 distance를 구해서 Matching 여부를 판단한다.
1) Detection : Image 내에서 같은 patch를 찾는다.
2) Description : Vector로 각 patch의 분포에 의한 벡터를 만드는 것
3) Match : 벡터를 비교하는 것
Feature Detection Procedure (특징 매칭 검출)
Local Feature 의 예시
1) Edge : 이미지 내의 Edge 검출
2) Corners : 이미지 내의 Corner부분 검출
3) Blob : Corner Point + Scale (Scale - Invariant Feature Transform ; SIFT)
Scale은 Corner Point의 반지름의 크기로서 존재한다.
4) Affine covariant regions
Local Feature Detector의 종류

Corner Feature Detector
Corner Feature : unique하고 특정적이다. 영상에서 다른 지점과 똑같은 patch가 나올 확률이 같다. lighting과 viewpoing가 변한다. edge를 따라서 움직인다면,
Harris Detector Formulation
I : SIFT 전 후로 같은 좌표에 해당하는 밝기좌표

전체 화소에 대해서 밝기 차이를 구하는 것이 아니라, w(xi)를 곱해서 Window 영역 내에서 구해준다.
Shift후 Window 내의 겹치는 부분에서 밝기 차이를 구해서 측정할 수 있다.
delta u 만큼 Shift가 이루어졌으며 Window안에서 Summation함으로써 Shift한 만큼의 밝기 값을 모든 화소에 대해서 구해서 합치는 것이다.
E가 큰 값이 나올수록 unique한 영상을 많이 얻을 수 있으므로 좋은 것이라 할 수 있다.

위와 같이 화소의 위치에 따라 밝기 값이 클수도 있고, 작을 수도 있다.
주로 Edge와 Corner포인트에서는 Eac의 값이 크게 측정된다.
이 화소마다의 밝기 값의 차이를 통해 Corner Point를 찾을 수 있다는 것이 핵심이다.
이것을 자동으로 찾기 위해, 테일러 급수를 이용해 위 식을 변형해보자.


이 행렬은 Eac를 구할 수 있는 중요한 키가 된다

Quadratic Form으로 쉽게 Eac를 구할 수 있게 되는데,
Matrix A에는 Flat한 경우, Corner의 경우, Edge의 경우 아래와 같이 분포한다.


아이겐 Value의 크기에 따라서 아래와 같이 분포를 달리할 수 있다.

eigen Value를 취득하여 현재 영역이 Flat, Corner, Edge인지 파악할 수 있다.
A는 대각 행렬이기 때문에,

Corner에 해당하는 Edge가 Align이 안되어있어도 P행렬에 의해서 Align할 수 있다.
이때 전제는 Eigen Value를 구한다는 것이고, 이 과정에서 Corner Point를 취득할 수 있다.
Corner Reponse Function

이 R이 어떤 threshold 값보다 크면 Corner Point라고 정한다.
Harris Detector : Properties
영상이 회전한 경우에도 동일하게 Corner Point를 검출할 수 있다.
- SIFT : 단점을 보완하기 위한 특정점 검출
Scale Invariant Function에 대해 Peak 지점을 얻음으로서 Automatic Scale Selection을 수행할 수 있다.
Laplacian-of-Gaussian
: Blob Detector, Point와 Scale(반지름)을 가지는 원형 모양을 찾는 Detector이다. LoG는 Blob의 크기에 맞게 Sigma값을 조정한다. 이렇게 Sigma 값을 조정함으로써 Blob의 크기에 맞추는 과정을 Scale Selection에 접목할 수 있다. 이를 LoG Filter로 구현할 수 있다. - Sigma가 클수록 Low pass쪽으로 수렴하는 Band Pass Filter이다. - Edge가 두껍고 Blob이 클수록 Reponse가 큰 Signal을 생성
SIFT (Scale Invariant Feature Transform)
Scale Space Detetction: 영상의 크기가 변하지 않고 여러가지 Fitler를 나열해 Scale을 조정한다. 이 특정 크기의 Filter들의 묶음을 한 Octave라고 표현하고, 
그림처럼 Image Pyramid의 형식으로 Scale Change를 Simulation한다.
DoG(Difference of Gaussian)
: 같은 Octave 내에 존재하는 서로 다른 Guassian Blurred Image로 빼기 연산을 수행해 DoG 이미지를 생성한다.
Nonmax-Suppression을 이용해 Extrema를 구할 수 있다.
Keypoint Localization
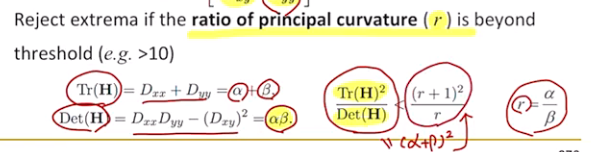
alpha와 beta가 균등하면 Edge가 아닐 가능성이 높다.
즉 ratio를 구해서 특정 Threshold와 비교해 Edge임을 구분할 수 있다.
여기서 eigen value를 구할 필요 없이, Determinant와 Trace만을 가지고 수식을 만들어서 Threshold식과 비교하면 됨!
Orientation Assignment
Gradient Orientation의 방향을 구하여 Histogram으로 정리, 가장 큰 값을 Edge의 방향으로 설정한다.
이 과정을 통해서 Edge의 위치, Scale, 방향(Orientation) 정보를 얻을 수 있다.
Descriptor은 수학적인 Vector의 형태로 표현된다.
SIFT는 128차원의 벡터로 표현되며 Image Gradient를 이용해서 영상의 Sub 영역 내부의 Keypoint descripor을 Histogram의 형태로 얻는다.
Final SIFT Features
하나의 SIFT는 아래를 포함한다.
128 dimensional descriptors(128차원의 벡터) , Scale, Orientation, 2D coordinates
Feature Description
SIFT는 Scale Invariant하게 Scale Selection을 수행하는 것이고,
Detector(LoG, DoG)을 통해 위치, 스케일, 방향을 구할 수 있다.
이를 128차원의 벡터로 표현하는 Description을 진행한다.
Harris Corner 주변에서 SIFT Detctor 파트와 Descriptor 파트를 분리해서 이해하기.
Feature Matching
물체가 변형되고 변화하고 있을 때 서로 다른 영상에서의 특징점을 검출해 대응되는 특징점들을 연결한다.
Threshold based matching
: multiple matches
Nearest neighbor matching (NN)
: Single match result
Nearst neighbor distance ratio(NNDR)

위 식을 토대로 distance를 구하여 Nearest Neighbor임을 확인할 수 있다.
Base metrics

1) TP (True Positive) : Number of Correct matches
2) FN (False Negative) : Matches that are incorrectly rejected
3) FP(False positive)
4) TN (True Negative)

3) PPV : '개'라고 판단된 것들 중에서 실제로 '개'인 것들
4) ACC : 실제 '개', '고양이' 전체 데이터에 대해서 정확히 판단한 정도
'Major Study > Digital Image Processing' 카테고리의 다른 글
| Lecture 11. Image Stitching (Panorama) (1) | 2022.06.09 |
|---|---|
| Lecture10. Image Transform (이미지 변환) (0) | 2022.06.09 |
| Lecture8 : Clustering and Segmentation (군집화와 영역화) (0) | 2022.06.03 |
| 주파수 영역 필터링(Filtering in Frequency Domain) (0) | 2022.04.05 |
| C++을 이용한 선형 필터링(Linear Filtering ) 구현하기 (0) | 2022.03.31 |
