큐, 스택, 데크
큐는 선입선출 (FIFO)의 속성을 가지고 있다. 스택(Stack) 은 반대로 후입선출(LIFO)의 속성을 가지고 있고, 데크(dequeue) 는 양쪽 끝에서 넣고 뺄 수 있는 자료 구조를 말한다.
이 자료 구조는 동적 배열, 혹은 연결 리스트로 구현할 수 있다
(1) 연결리스트로 구현 시 양쪽 끝에서 상수 시간에 추가와 삭제가 가능하다.
(2) 동적 배열을 이용한 구현 시, 배열의 맨 앞에서 원소 삭제 시 O(n)의 시간이 걸린다는 단점이 있다 → head와 tail을 이용해서 이 점을 보완할 수 있다.
즉 배열 전체가 아닌 head부터 tail까지만 자료구조로 사용하겠다는 건데, 버려지는 공간이 많다는 단점이 있다. 이는 환형 버퍼 (circular buffer) 의 개념으로 해결할 수 있는데, 동적 배열이 끝까지 사용되면 다시 앞으로 돌아와 처음부터 할당하는 것이다.
예제 : 울타리 자르기(스위핑 알고리즘)
#include <iostream>
#include <vector>
#include <stack>
using namespace std;
vector<int> h; // 판자의 높이를 저장하는 배열
int solveStack() {
stack<int> remaining; // 남아있는 판자들의 위치
h.push_back(0);
int ret = 0;
for (int i = 0; i < h.size(); i++) {
// 현재 판자의 위치에서 남아있는 판자의 높이가 더 높은 경우에
while (!remaining.empty() && h[remaining.top()] >= h[i]) {
int j = remaining.top();
remaining.pop(); // 제거한다.
int width = -1;
if (remaining.empty())// 남은 판자가 하나도 없는 경우 left[j] = -1
width = i; // 넓이는 현재 판자까지의 전체
else
width = (i - remaining.top() - 1); // 제일 오른쪽 판자와의 거리
// lef[j] = 남아있는 판자 중 가장 가까이 있는 판자의 번호
ret = max(ret, h[j] * width); // 넓이의 최대를 구한다.
}
remaining.push(i);
}
return ret;
}문제 : 외계 신호 분석
모든 키를 메모리에 올리지 않고 일부만 사용하는 온라인 알고리즘을 사용하고 있다. 즉 모든 입력을 다 받은 상태가 아니어도 알고리즘을 동작할 수 있는 것이다.
(1) 모든 부분 수열을 모두 검사하면서 합이 K인 수열을 찾는 방법
int simple(const vector<int>& signals, int k) {
int ret = 0;
for (int head = 0; head < signals.size(); head++) {
int sum = 0;
for (int tail = head; tail < signals.size(); tail++) {
// sum은 [head, tail]의 구간 합이다.
sum += signals[tail];
if (sum == k) ret++;
if (sum >= k) break;
}
}
return ret;
}head와 tail을 지정해서 그 구간을 순회하며 sum을 구하고 있다. 이 알고리즘의 시간 복잡도는 O(NK)이다.
이 알고리즘을 자세히 보면, tail은 head가 시작하는 지점부터 for문을 돌고 있지만 실상은, “이전 탐색에서 만든 부분 구간에서의 tail”에서 “그 다음 탐색에서 만든 부분 구간의 tail”이 더 줄어드는 경우는 없다는 것이다.
왜냐하면, head가 증가하는데 tail이 감소하게 되면 그 이전 부분 구간의 부분 구간이 되기 때문에 당연히 ! k보다 작은 것이 저명하기 때문이다.
따라서 우리는 tail을 이전 단계에서 정한 tail부터 지정해도 상관이 없는 것이다
int optimized(const vector<int>& signals, int k) {
int ret = 0, tail = 0, rangeSum = signals[0];
for (int head = 0; head < signals.size(); head++) {
// rangeSum이 k이상인 최초의 구간을 만날 때까지 tail을 옮긴다.
while (rangeSum < k && tail + 1 < signals.size())
rangeSum += signals[++tail];
if (rangeSum == k) ret++;
// signals[head]는 이제 구간에서 빠지게 된다.
// => 구간합을 새로 계산할 필요가 없음 !!
rangeSum -= signals[head];
}
return ret;
}분할 상환 분석을 이용해 이 알고리즘의 시간 복잡도를 계산하면 O(N)이다.
왜? 지금 while문은 최대 N번 동작한다. tail은 head(초기값 0) 부터 n까지의 범위를 가지고 있기 때문이다. 분할 상환 분석은 모든 연산들이 수행되는 동안 각 연산의 평균적인 수행 시간을 분석하는 방법을 의미한다.
길이가 N인 시퀀스가 있을 때, 아래를 만족하는 전체 수행 시간의 적절한 상한 T(n)을 찾아보자.ci는 i번째 연산을 수행할 때 필요한 시간이다.
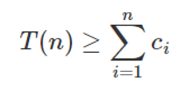
대개는 T(n)/n이 최악의 경우에도 평균적인 연산의 수행 시간이 된다. 이를 합계 분석 (aggregate analysis) 방식이라고 한다.
이제 온라인 알고리즘으로 바꿔보면,
head가 증가한 이후 이미 지나친 숫자들은 더 이상 고려할 필요가 없다. 지금 검사하고 있는 후보 구간에 있는 숫자들만이 메모리 저장 대상이다.
struct RNG {
unsigned seed; // pow(2, 32)로 나눈 나머지를 처리할 필요가 없다.
RNG() : seed(1983) {}
unsigned next() {
unsigned ret = seed;
seed = ((seed * 214013u) + 2531011u);
return ret % 10000 + 1;
}
};
int countRanges(int k, int n) {
RNG rng;
queue<int> range; // 현재 구간에 들어있는 숫자들을 저장하는 큐
int ret = 0, rangeSum = 0;
for (int i = 0; i < n; i++) {
int newSignal = rng.next(); // 구간에 숫자를 추가한다.
rangeSum += newSignal;
range.push(newSignal);
// 구간의 합이 k를 초과하는 동안 구간에서 숫자를 뺀다.
while (rangeSum > k) {
rangeSum -= range.front();
range.pop();
}
if (rangeSum == k) ret++;
}
return ret;
}queue 로 구현한 이유는, 부분 구간을 변경할 때마다 head와 tail은 뒤로 이동하므로, 제일 앞의 숫자는 빠지고 뒤의 숫자가 추가되는 구조이기 때문이다. 이는 queue와 유사해서 위에서처럼, 그때그때 newSignal을 구한 뒤 push하는 방식으로 구현할 수 있다.
그리고 다시 역행하여 K보다 작거나 같아질 때까지 구간에서 숫자를 빼는 것이다 !!
'Algorithm > Algospot' 카테고리의 다른 글
| [Algorithm] 선형 자료구조 #230212 (0) | 2023.03.23 |
|---|---|
| [Algorithm] 부분합 (partial sum) #230212 (0) | 2023.03.23 |
| [Algorithm] 비트마스크 (Bit-mask) #230210 (1) | 2023.03.22 |
| [Algorithm] 동적 계획법 (Dynamic Programming) #230203 (1) | 2023.03.13 |
| [Algorithm] 분할 정복 (Divide & Conquer) #230202 (0) | 2023.03.13 |
큐, 스택, 데크
큐는 선입선출 (FIFO)의 속성을 가지고 있다. 스택(Stack) 은 반대로 후입선출(LIFO)의 속성을 가지고 있고, 데크(dequeue) 는 양쪽 끝에서 넣고 뺄 수 있는 자료 구조를 말한다.
이 자료 구조는 동적 배열, 혹은 연결 리스트로 구현할 수 있다
(1) 연결리스트로 구현 시 양쪽 끝에서 상수 시간에 추가와 삭제가 가능하다.
(2) 동적 배열을 이용한 구현 시, 배열의 맨 앞에서 원소 삭제 시 O(n)의 시간이 걸린다는 단점이 있다 → head와 tail을 이용해서 이 점을 보완할 수 있다.
즉 배열 전체가 아닌 head부터 tail까지만 자료구조로 사용하겠다는 건데, 버려지는 공간이 많다는 단점이 있다. 이는 환형 버퍼 (circular buffer) 의 개념으로 해결할 수 있는데, 동적 배열이 끝까지 사용되면 다시 앞으로 돌아와 처음부터 할당하는 것이다.
예제 : 울타리 자르기(스위핑 알고리즘)
#include <iostream>
#include <vector>
#include <stack>
using namespace std;
vector<int> h; // 판자의 높이를 저장하는 배열
int solveStack() {
stack<int> remaining; // 남아있는 판자들의 위치
h.push_back(0);
int ret = 0;
for (int i = 0; i < h.size(); i++) {
// 현재 판자의 위치에서 남아있는 판자의 높이가 더 높은 경우에
while (!remaining.empty() && h[remaining.top()] >= h[i]) {
int j = remaining.top();
remaining.pop(); // 제거한다.
int width = -1;
if (remaining.empty())// 남은 판자가 하나도 없는 경우 left[j] = -1
width = i; // 넓이는 현재 판자까지의 전체
else
width = (i - remaining.top() - 1); // 제일 오른쪽 판자와의 거리
// lef[j] = 남아있는 판자 중 가장 가까이 있는 판자의 번호
ret = max(ret, h[j] * width); // 넓이의 최대를 구한다.
}
remaining.push(i);
}
return ret;
}문제 : 외계 신호 분석
모든 키를 메모리에 올리지 않고 일부만 사용하는 온라인 알고리즘을 사용하고 있다. 즉 모든 입력을 다 받은 상태가 아니어도 알고리즘을 동작할 수 있는 것이다.
(1) 모든 부분 수열을 모두 검사하면서 합이 K인 수열을 찾는 방법
int simple(const vector<int>& signals, int k) {
int ret = 0;
for (int head = 0; head < signals.size(); head++) {
int sum = 0;
for (int tail = head; tail < signals.size(); tail++) {
// sum은 [head, tail]의 구간 합이다.
sum += signals[tail];
if (sum == k) ret++;
if (sum >= k) break;
}
}
return ret;
}head와 tail을 지정해서 그 구간을 순회하며 sum을 구하고 있다. 이 알고리즘의 시간 복잡도는 O(NK)이다.
이 알고리즘을 자세히 보면, tail은 head가 시작하는 지점부터 for문을 돌고 있지만 실상은, “이전 탐색에서 만든 부분 구간에서의 tail”에서 “그 다음 탐색에서 만든 부분 구간의 tail”이 더 줄어드는 경우는 없다는 것이다.
왜냐하면, head가 증가하는데 tail이 감소하게 되면 그 이전 부분 구간의 부분 구간이 되기 때문에 당연히 ! k보다 작은 것이 저명하기 때문이다.
따라서 우리는 tail을 이전 단계에서 정한 tail부터 지정해도 상관이 없는 것이다
int optimized(const vector<int>& signals, int k) {
int ret = 0, tail = 0, rangeSum = signals[0];
for (int head = 0; head < signals.size(); head++) {
// rangeSum이 k이상인 최초의 구간을 만날 때까지 tail을 옮긴다.
while (rangeSum < k && tail + 1 < signals.size())
rangeSum += signals[++tail];
if (rangeSum == k) ret++;
// signals[head]는 이제 구간에서 빠지게 된다.
// => 구간합을 새로 계산할 필요가 없음 !!
rangeSum -= signals[head];
}
return ret;
}분할 상환 분석을 이용해 이 알고리즘의 시간 복잡도를 계산하면 O(N)이다.
왜? 지금 while문은 최대 N번 동작한다. tail은 head(초기값 0) 부터 n까지의 범위를 가지고 있기 때문이다. 분할 상환 분석은 모든 연산들이 수행되는 동안 각 연산의 평균적인 수행 시간을 분석하는 방법을 의미한다.
길이가 N인 시퀀스가 있을 때, 아래를 만족하는 전체 수행 시간의 적절한 상한 T(n)을 찾아보자.ci는 i번째 연산을 수행할 때 필요한 시간이다.
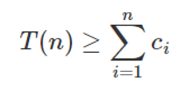
대개는 T(n)/n이 최악의 경우에도 평균적인 연산의 수행 시간이 된다. 이를 합계 분석 (aggregate analysis) 방식이라고 한다.
이제 온라인 알고리즘으로 바꿔보면,
head가 증가한 이후 이미 지나친 숫자들은 더 이상 고려할 필요가 없다. 지금 검사하고 있는 후보 구간에 있는 숫자들만이 메모리 저장 대상이다.
struct RNG {
unsigned seed; // pow(2, 32)로 나눈 나머지를 처리할 필요가 없다.
RNG() : seed(1983) {}
unsigned next() {
unsigned ret = seed;
seed = ((seed * 214013u) + 2531011u);
return ret % 10000 + 1;
}
};
int countRanges(int k, int n) {
RNG rng;
queue<int> range; // 현재 구간에 들어있는 숫자들을 저장하는 큐
int ret = 0, rangeSum = 0;
for (int i = 0; i < n; i++) {
int newSignal = rng.next(); // 구간에 숫자를 추가한다.
rangeSum += newSignal;
range.push(newSignal);
// 구간의 합이 k를 초과하는 동안 구간에서 숫자를 뺀다.
while (rangeSum > k) {
rangeSum -= range.front();
range.pop();
}
if (rangeSum == k) ret++;
}
return ret;
}queue 로 구현한 이유는, 부분 구간을 변경할 때마다 head와 tail은 뒤로 이동하므로, 제일 앞의 숫자는 빠지고 뒤의 숫자가 추가되는 구조이기 때문이다. 이는 queue와 유사해서 위에서처럼, 그때그때 newSignal을 구한 뒤 push하는 방식으로 구현할 수 있다.
그리고 다시 역행하여 K보다 작거나 같아질 때까지 구간에서 숫자를 빼는 것이다 !!
'Algorithm > Algospot' 카테고리의 다른 글
| [Algorithm] 선형 자료구조 #230212 (0) | 2023.03.23 |
|---|---|
| [Algorithm] 부분합 (partial sum) #230212 (0) | 2023.03.23 |
| [Algorithm] 비트마스크 (Bit-mask) #230210 (1) | 2023.03.22 |
| [Algorithm] 동적 계획법 (Dynamic Programming) #230203 (1) | 2023.03.13 |
| [Algorithm] 분할 정복 (Divide & Conquer) #230202 (0) | 2023.03.13 |
