1003번: 피보나치 함수
각 테스트 케이스마다 0이 출력되는 횟수와 1이 출력되는 횟수를 공백으로 구분해서 출력한다.
www.acmicpc.net


#include <iostream>
#define endl '\n'
using namespace std;
int fibonacci(int n, int &cnt0, int &cnt1) {
if (n == 0) {
cnt0++;
return 0;
}
else if (n == 1) {
cnt1++;
return 1;
}
else {
return fibonacci(n - 1, cnt0, cnt1) + fibonacci(n - 2, cnt0, cnt1);
}
}
int main() {
ios_base::sync_with_stdio(false);
cin.tie(NULL);
int t; cin >> t;
for (int i = 0; i < t; i++) {
int cnt0 = 0;
int cnt1 = 0;
int n; cin >> n;
fibonacci(n, cnt0, cnt1);
cout << cnt0 << " " << cnt1 << endl;
}
return 0;
}처음에는 이렇게 재귀적으로 코드를 작성하고, cnt0과 cnt1 파라미터를 Call by Reference로 넘기는 방식으로 구현하였다.
그러나 n=40을 넣었을 때 2^40의 연산으로 시간 초과가 발생하는 문제가 있어서, 동적 계획법으로 코드를 변경하였다.
메모이제이션
재귀로 fibonacci를 수행하면 n이 커질 수록 반복적으로 계산하는 수가 많아진다. 메모이제이션 기법을 활용해, 이전에 계산한 값을 기억해두었다가 바로 다음 계산에서 활용하는 방식으로 구현할 수 있다.
상향식, 하향식 구현으로 나눌 수 있는데, 나는 먼저 해결한 하위 문제를 통해 복잡한 상위 문제를 해결하는 상향식 구현을 사용했다.
int fibonacci(int n) {
vector<int> val = { 0, 1 };
if (n >= 2) {
for (int i = 2; i <= n; i++) {
val.push_back(val[i - 1] + val[i - 2]);
}
}
return val[n];
}그렇게 구현한 fibonacci는 위와 같다.
입력값이 0과 1인 경우에만 예외처리하고, DP를 이용해 피보나치를 구현하는 과정에서 return 0 혹은 1을 수행하는
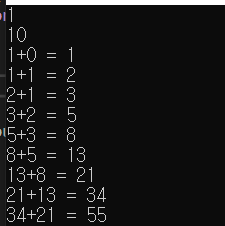
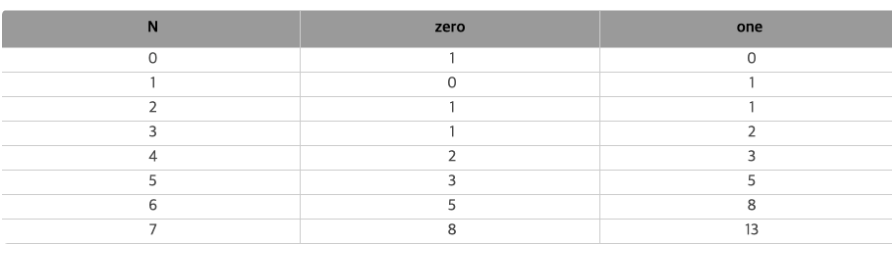
n = 10으로 두고 val[i -1]과 val[i-2]의 합 = val[i]를 출력한 결과이다. 아래 표를 참고해봤을 때 0과 1의 개수는 해당 N에 대해서 각각 val[N - 1]과 val[N]을 의미한다.
정답 코드는 아래와 같다.
#include <iostream>
#include <vector>
#define endl '\n'
using namespace std;
void fibonacci(int n) {
vector<int> val = {0, 1};
if (n == 0) {
cout << 1 << " " << 0 << endl;
}
else if (n == 1) {
cout << 0 << " " << 1 << endl;
}
else { // n >= 2인 경우
for (int i = 2; i <= n; i++) {
val.push_back(val[i - 1] + val[i - 2]);
}
cout << val[n - 1] << " " << val[n] << endl;
}
}
int main() {
ios_base::sync_with_stdio(false);
cin.tie(NULL);
int t; cin >> t;
for (int i = 0; i < t; i++) {
int n; cin >> n;
fibonacci(n);
}
return 0;
}
'Algorithm > Baekjoon' 카테고리의 다른 글
| 백준 12847 꿀 아르바이트 C++ 풀이 (0) | 2022.11.09 |
|---|---|
| 백준 1806 부분합 C++ 풀이 (0) | 2022.11.09 |
| [BOJ]9934 : 완전 이진 트리 C++ 문제 풀이 (0) | 2021.11.04 |
| [BOJ]10773 제로 : 스택과 큐 C++ 문제풀이 (0) | 2021.09.18 |
| [BOJ]11399 ATM : 그리디 알고리즘 C++ 문제풀이 (0) | 2021.03.09 |
