(1) BubbleSort
ExchangeSort라고도 함.6t
배열을 쭉 순회하면서 현재 인덱스의 요소를 기준으로 뒤에 있는 요소들을 한 번씩 순회
큰 요소(내림차순), 작은 요소(오름차순) 이 있다면 swap하며 정렬을 수행한다.
void bubbleSort(int* a, int size) {
int i, j;
for (int i = 0; i < size -1; i++) {
for (int j = i + 1; j < size; j++) {
if (a[j] > a[i]) {
swap(a[j], a[i]);
}
}
}
}if문에서 a[j]가 더 크면 내림차순 정렬이다. 왜냐하면 큰 요소를 앞으로 가져온다는 뜻이기 때문이다.
(2) Insertion Sort
Sorting되고 있는 구간, Sort되지 않은 구간을 나누어
non-Sorting구간에서 차례로 요소를 하나씩 빼와 Sorting구간과 하나하나 비교해준다.
오름차순 정렬일 경우, 빼온 요소가 Sorting구간의 요소보다 작다면 그 작음을 발견한 인덱스 앞에 끼워넣어준다.
void insertionSort(int* arr, int size) {
int i, j;
int x;
// 0번째는 Sort되어있다고 가정하고 시작
for (int i = 1; i < size; i++) {
x = arr[i]; // arr[i]의 값 미리 담아두어야 함.
j = i - 1; // Sorted되지 않은 배열과 가장 인접한 Sorting된 배열의 인덱스
while (j >= 0 && arr[j] > x) {
arr[j + 1] = arr[j];
j--;
}
arr[j + 1] = x;
}
}
(3) Selection Sort
제일 처음 값을 최솟값이라고 두고, 다음 인덱스부터 순차적으로 순회한다.
순회하면서 제일 최솟값을 찾아 제일 앞에 있던 인덱스와 swap한다.
그리고 두번째 인덱스를 다시 최솟값으로 지정하여 다음 인덱스부터 다시 순회하면서 swap한다.
void selectionSort(int* arr, int size) {
int minIndex;
for (int i = 0; i < size - 1; i++) {
minIndex = i;
for (int j = i + 1; j < size; j++) {
if (arr[j] < arr[minIndex]) { // 여기 등호 바꾸면 내림차순
minIndex = j;
}
} // 여기까지 최솟값 찾는 알고리즘
swap(arr[minIndex], arr[i]); // 처음에 최솟값이라 생각했던 것과 바꿔준다.
}
}max값을 찾냐, min값을 찾냐는 순회하면서 인덱스를 저장해주는 시기가 더 '큰' 것이 발견되었을 때냐,
'작은' 것이 발견되었을 때냐로 결정된다.
즉 if문에서 부등호만 바꾸어주면 기준으로 정한 index보다 크면 갱신하여주기 때문에 max값이 매 순회 찾아지게 되고,
처음 인덱스와 swap해줌으로써 내림차순 정렬이 완성된다.
(4) MergeSort
void merge(int h, int m, int* U, int* V, int* S) {
int i = 0, j = 0, k = 0;
while (i < h && j < m) {
if (U[i] < V[j]) {
S[k] = U[i];
i++;
}
else {
S[k] = V[j];
j++;
}
k++;
}
if (i >= h) { // U배열의 순환이 끝난 경우
while (j != m) {
S[k] = V[j];
j++, k++;
}
}
else { // V 배열의 순환이 끝난 경우
while (i != h){
S[k] = U[i];
i++, k++;
}
}
}
void mergeSort(int* arr, int size) {
int h = size / 2;
int m = size - h;
int* U = new int[h];
int* V = new int[m];
if (size > 1) {
for (int i = 0; i < h; i++) {
U[i] = arr[i];
}
for (int i = 0; i < m; i++) {
V[i] = arr[i + h];
}
mergeSort(U, h);
mergeSort(V, m);
merge(h, m, U, V, arr);
}
}코드를 짜면서 아래 시행착오를 겪었다.
1) mergeSort() 재귀호출 및 merge() 호출을 if문 밖에서 수행해주어 중단점이 실행되지 않아 StackOverflow
2) merge함수에서 while 조건문을 i <= h && j <= m으로 설정, array OutOfBound 에러 발생
배열 요소 시작이 1부터인 경우 등호를 붙여주어야 한다.

여기 사후 처리 하는 코드에서도 마찬가지.
if문이 i >= h로 되어있는데, 인덱스가 1부터 시작한 경우는 i가 h와 같은 경우에도
배열의 순환이 끝났다고 판단하지 않고 while문을 수행해준다.
점화식으로 MergeSort의 시간 복잡도 계산
만약에 h 가 n /2가 아니라 n/4인 경우
Tn/4이 4번 실행된다. 이때 점화식을 계산하면 치환되는 i의 값은 log_2가 아니라 log_4가 된다!
h = n/4인 경우의 점화식 시간 복잡도 계산하기
공간 복잡도 ?
log n의 크기의 높이의 머시기
(5) QuickSort
1) 임의로 pivot을 설정한다. 예제에서는 제일 끝의 요소를 pivot으로 정하였다.
2) 제일 앞의 요소를 left, pivot 앞의 요소를 right라고 지정
3) left는 오른쪽으로 이동하다가 pivot보다 크면 멈추고, right는 왼쪽으로 이동하다 pivot보다 작으면 멈춘다.
3) left와 right가 모두 멈춰지면 arr[left]와 arr[right]를 swap
4) left와 right가 겹쳐지거나, right와 left가 교차된 경우 left와 pivot의 위치만 바꿔주고 순회를 종료한다.
5) pivot을 기준으로 왼쪽, 오른쪽 배열을 재귀호출하여 quickSort를 수행한다.
left는 pivot보다 크면 멈춰있는 놈이다.
순회가 종료되었을 때 left와 right가 교차되었든 말든 마지막으로 left와 right는 자신의 의무를 수행했다.
즉, pivot보다 큰 위치에, 혹은 작은 위치에 멈춰있다.
우리는 pivot을 기준으로 왼쪽,오른쪽으로 나누어 재귀호출을 수행할 것이므로,
pivot보다 큰 left를 오른쪽으로 넘겨버리고 재귀호출하는 것이다.
void quickSort(int* arr, int start, int end) {
if (start >= end) return;
int pivot = arr[end];
int left = start;
int right = end - 1;
while (left <= right) {
while (left <= right && arr[left] <= pivot)
left++;
while (left <= right && arr[right] >= pivot)
right--;
if (left < right)
swap(arr[left], arr[right]);
}
swap(arr[left], arr[end]);
quickSort(arr, start, left - 1);
quickSort(arr, left + 1, end); // left자리에 pivot이 위치함
}여기서 한 실수는 마지막에 while문이 종료되고 swap할 때 arr[end] 대신에 pivot을 넣은 것이다.
end의 값은 매개변수로 들어가 계속 변하기 때문에 arr[end]를 그대로 사용하여야 한다.
(엥 그래도 매 호출마다 pivot값을 end 인덱스로 초기화해주니까 상관 없는 거 아닌가?)
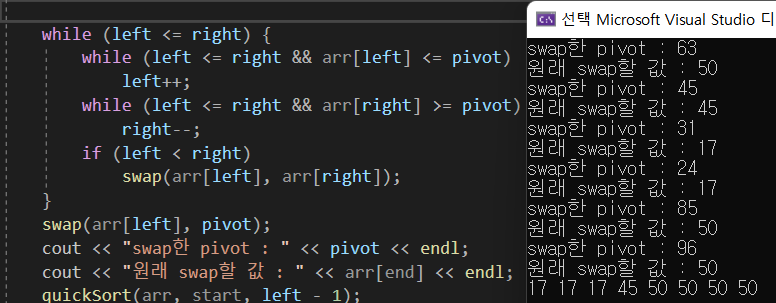
출력해보니 엄연히 다른 값을 가지고 있었다.
위에 while문 안에서 swap을 하면서 값이 바뀌었기 때문이라고 예상하였다.
QuickSort의 성능 향상 방법
1. 순환 제거 : 스택을 사용해서 순환을 제거
2. 작은 부분화일 : 파티션의 크기가 임의로 정한 크기 M보다 작으면 n^2 알고리즘(삽입 정렬)을 사용해 정렬
3. 중간값 분할 : 임의로 세개의 원소를 골라, 그 중에 중간값을 선택해서 pivot으로 사용
MergeSort와 QuickSort의 구분
1) MergeSort : 분할-정복(Divide and Conquer), 배열을 먼저 분할하고 각각 개별적으로 정렬한 후 합친다. + Stable함
2) QuickSort : 순환 호출이 이루어지기 전에 정렬이 수행된다. + Stable하지 않을 수 있음
(6) Shell Sort
삽입 정렬의 변형, 사용자가 증가, 감소의 크기를 지정해서 홀수, 짝수를 반복하며 h번째 원소를 정렬한다.
정한 gap만큼 배열에서 요소를 띄엄띄엄 꺼내와서 모아 삽입 정렬한다. 정렬된 값을 그대로 다시 꺼내온 자리에 넣고, 이를 반복해 모든 원소에 대해 정렬을 수행함.
void shellSort(int* arr, int size) {
int h;
for (h = 0; h < size; h = 3 * h + 1) {} // 첫 번째 h의 값 계산
for (; h > 0; h /= 3) {
for(int i = h + 1; i <= size; i++){
int v = arr[i];
int j = i;
while (j > h && arr[j - h] > v) {
arr[j] = arr[j - h];
j = j - h;
}
arr[j] = v;
}
}
}
'Algorithm' 카테고리의 다른 글
| 다익스트라(Dijkstra) 알고리즘의 개념 (0) | 2022.03.21 |
|---|---|
| 프림 알고리즘의 개념 (0) | 2022.03.21 |
| [C++] BFS와 DFS 개념 정리 (0) | 2022.03.14 |
| [C++] 구글폼 복수응답 날짜 별로 응답자 정리하는 프로그램 (0) | 2022.03.13 |
| 그리디 알고리즘(Greedy Algorithm)의 개념, 예제 코드 (0) | 2022.03.06 |
