1. 개요
정렬 알고리즘을 배운 것을 토대로 아래 네 가지 정렬 알고리즘을 만들고, 다양한 Case를 나누어 프로그램의 동작 방식을 이해하는 과제이다.
프로젝트 파일의 구성도는 다음과 같다.
1) SortAlgorithm.h
Insertion Sort, Selection Sort, Merge Sort, Quick Sort를 수행하는 네 가지 알고리즘을 구현한 파일이다. 이때 이전에 구현한 ArrayVector와 그 내장함수를 사용하여 정렬할 배열을 선언하였다.
- Insert/ InsertionSort : 삽입 정렬
- SelectionSort : 선택 정렬
- Merge/ MergeSort : 합병 정렬
- QuickSort : 빠른 정렬
- Swap/printVector : 두 개의 값을 바꾸는 Swap 함수와, ArrayVector 내의 값을 출력하는 printVector함수
2) ArrayVector.h
이전 과제에서 만든 ArrayVector 코드에서, 프로그램을 구현하기 위한 목적에 맞추어 리뉴얼하였다. 추가된 함수 및 코드는 다음과 같다.
- Copy(ArrayVector<T> &S); : ArrayVector간의 값을 복사하기 위한 함수
- ArrayVector(const initializer_list<T>&list); : Initializer_list형태로 대입하기 위하여 만든 함수
- Struct Pair; : <key,value> 형태를 다루기 위해 선언
- Bool operator (비교연산자)(const Pair & a, const Pair &b); : 정렬 알고리즘 내에서 template T에 Pair타입이 들어왔을 경우, 비교 연산을 수행하기 위한 연산자 오버로딩
- Ostream& operator << (ostream& a, const Pair &b); : “cout << (Pair 객체)” 코드를 정상적으로 실행하기 위한 출력 연산자 오버로딩
3) Driver.cpp
실제 동작을 보여주는, main 함수가 포함된 파일이며 보고서에서 주어진 목적을 달성할 수 있는 함수들이 있다.
void print_sorted_ArrayVector(); : 정렬 알고리즘이 정상 도작하는 지 보여주는 함수
void verify_stable_Algorithm(); : 각 알고리즘이 Stable한 지 보여주는 함수
ArrayVector<int> generate_random_ArrayVector(int = 10); : random하게 매개변수에 들어온 size만큼 ArrayVector를 생성, 초기화해주는 함수
void compare_Algorithm(int = 10); : 각 정렬 알고리즘의 Sorting 시간을 계산하여 보여주는 함수
2. 구현상 특징
(1) 네 가지 알고리즘의 정렬 방식
- Insertion Sort

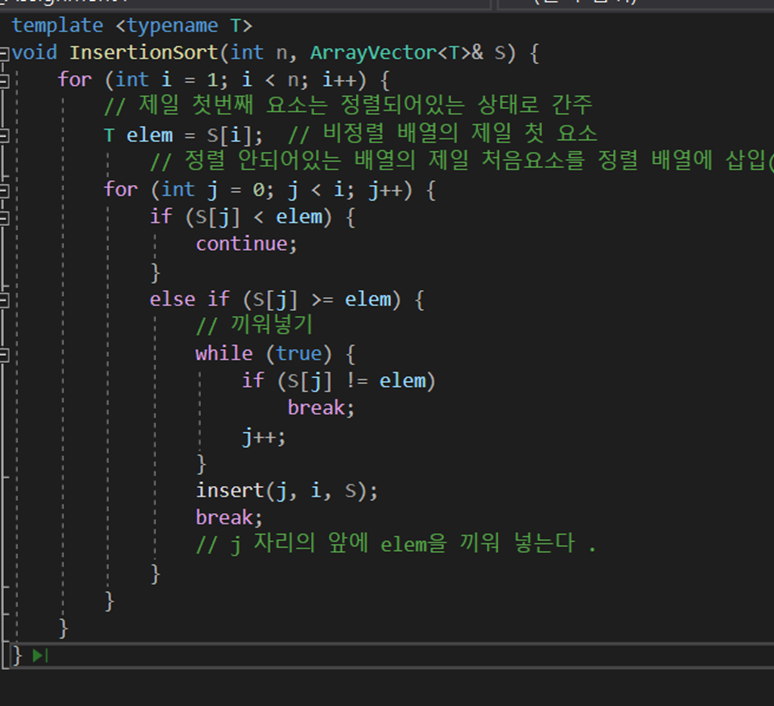
Insertion Sort에서는 하나의 배열을 정렬된 배열/정렬되지 않은 배열로 나누어서 정렬되지 않은 배열의 첫 번째 요소를 정렬된 배열에서 순차적으로 탐색하여 INSERT하는 방식으로 정렬한다.
이 코드 같은 경우에는 배열을 받아 for문을 돌면서 Insert할 곳을 탐색하는 insertionSort와 실제로 받아온 원소를 해당 인덱스의 앞 부분에 Insert하는 함수를 구분하였다. 이렇게 구현하였더니 코드가 간결해지는 이점이 있었으며, ArrayVector로 구현해 멤버 변수 A에 대한 변화가 한 눈에 들어오는 것을 알 수 있다.
- Selection Sort

Selection Sort는 처음에 제일 첫 번째 요소로 최솟값을 정한 뒤 배열을 순회하며, 현재의 smallest 변수의 값보다 더 작은 것이 존재한다면 그것을 다시 smallest로 정하면서 최솟값을 찾는 알고리즘을 이용하였다.
그리고 현재 기준으로 두고 순회를 돌고 있는 i번째 인덱스에 위치한 값과 smallest 값을 swap하여 작은 수는 앞에, 큰 수는 뒤에 놔둘 수 있게끔 설계하였다.
- MergeSort
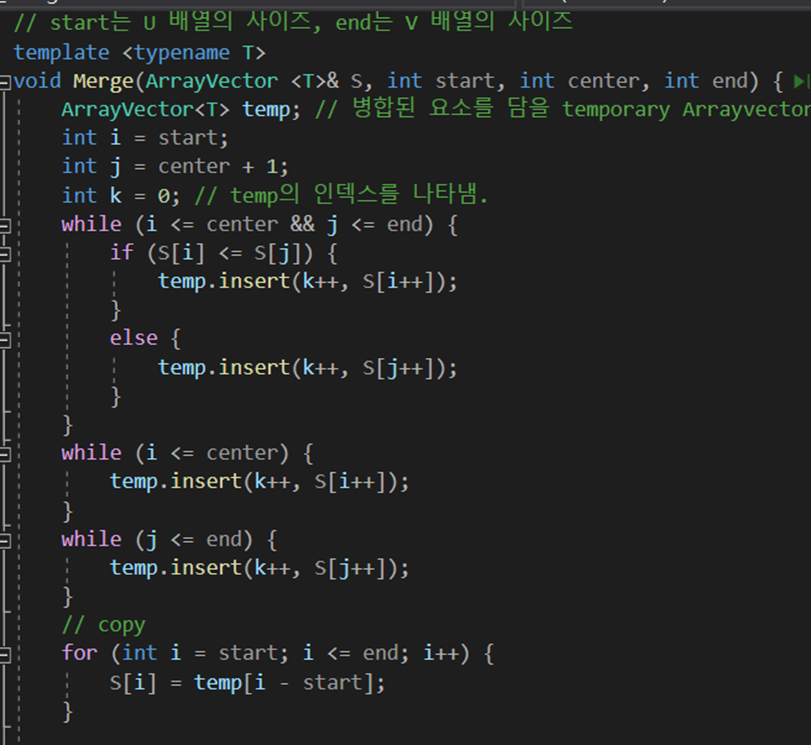
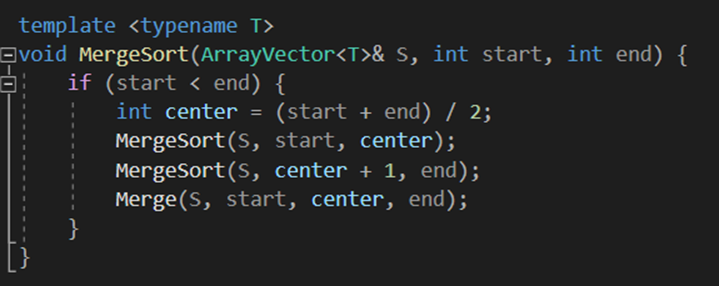
Merge Sort는 구현 과정에서 많은 시간과 노력을 든 알고리즘이다. ‘재귀 호출’의 개념이 도입된 함수이기 때문에 함수 Call과 반환, 중단점 조건 등을 세밀하게 고려해야했기 때문이다.
나는 위의 InsertionSort와 유사하게 mergeSort와 실제로 병합을 진행하는 merge함수를 구분하였다. 배열의 처음과 끝의 인덱스를 나타내는 변수, 그리고 ArrayVector의 객체를 매개변수에 넣어서 MergeSort 함수를 재귀호출 해 다시 왼쪽, 오른쪽으로 양분하는 알고리즘을 설계했다. 이렇게 배열의 크기가 점점 줄어들면서 스택에 함수 Call 이 쌓이게 되고, 크기가 1일 때 start = end가 되어 중단점을 충족하게 되었다.
그렇게 함수 Call을 빠져나오면 Merge 함수를 만나게 되는데, 여기서 나는 강의노트의 코드와는 다르게 전체 배열인 S를 매개변수로 받았다. 그리고 temp라는 정렬된 요소를 넣을 임시의 ArrayVector를 정의하였고 I, j 인덱스를 따로 두어서 왼쪽 배열, 오른쪽 배열을 구분하였다.
그리고 i와 j를 증가시키면서 작은 쪽을 temp 객체에 넣었다. 이렇게 함수 Call을 모두 아래 방향으로 거치고 나면 temp에는 정렬된 형태의 데이터가 담겨 있게 된다.
- QuickSort
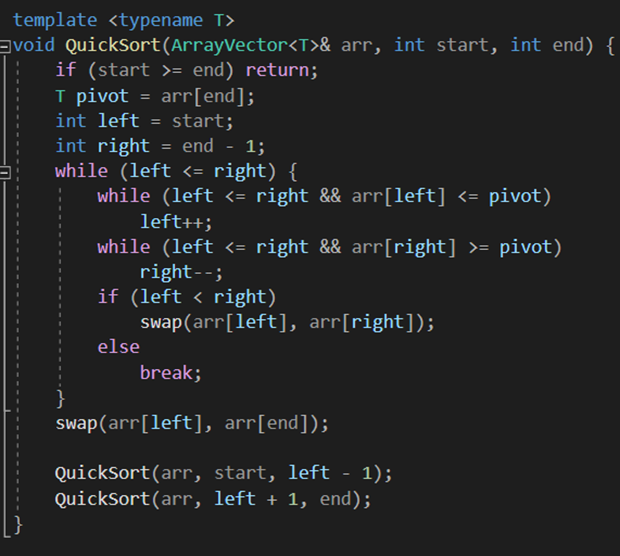
다음은 QuickSort이고, Pivot을 설정하는 방식은 배열의 제일 오른쪽에 있는 값을 항상 pivot으로 두고 알고리즘을 설계했다.
여기서도 start, end 변수를 생성해 start는 오른쪽으로, end는 왼쪽으로 순회를 돌면서 pivot의 값과 비교해 swap을 하는 방식으로 동작한다. 역시 재귀함수를 사용해, left 값을 기준으로 양분하여 크기가 1이 될 때까지 함수 Call을 진행하였다. 이때의 중단점은 left가 right보다 커졌을 때가 되겠고, 매 함수 Call마다 pivot값은 해당 배열에서의 가장 오른쪽 값이 되었다.
(2) 알고리즘 별 Stable/Un-Stable한 이유
- Insertion Sort è Stable

insertionSort 함수에서 정렬 배열의 순회를 돌다 삽입해야할 인덱스 부분을 마주쳤을 때의 코드를 보면 알 수 있다. while문이 사용되었고, 비정렬 배열의 첫번째 요소인 elem의 값과 일치하는 동안 j++;를 수행하는 것을 알 수 있다. 이 이유는 insert를 하다가 뒤에 있는 배열이 앞에 있는 정렬 배열에 insert 될 때 같은 값이 있는 경우 한 번 더 인덱스를 옮긴 뒤 삽입되어야 하기 때문이다.
- SelectionSort è UnStable
Selection Sort의 경우, smallest를 탐색하다가 같은 Key를 가진 요소가 나왔을 때 그냥 건너뛰고, 더 작은 요소와 Swap하게 된다. 이 때 ‘더 작은 요소’가 ‘같은 Key를 가진 요소’보다 앞에 있냐, 뒤에 있냐에 따라서 같은 Key들은 원래 그대로 정렬될 수도 있고, 순서가 바뀔 수도 있다.
이 논리에 따르면, 알고리즘이 Stable한 것을 코드 상에서 순수하게 구현할 수 없기 때문에 Selection Sort는 Unstable하다고 판단된다.
- MergeSort è Stable
MergeSort의 경우 아주 Stable하다고 할 수 있는데, 이 이유는 간단하다. 먼저 배열은 앞에서부터 순회하며, 하나씩 비교한다음 작을 경우 새로운 배열에 넣는 형태로 진행된다. 따라서 양분된 배열에 같은 Key값을 가진 요소가 따로 들어있다면, 먼저 확인된 요소가 temp 배열에 들어오는 것은 당연하다.
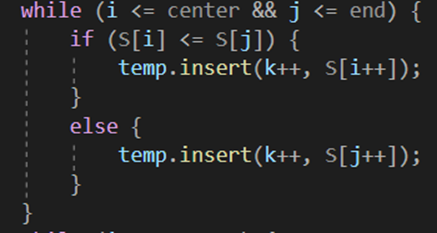
설령, 최악의 경우 배열의 크기가 1인 함수 Call이 진행되었을 때마저 같은 Key값을 가진 요소끼리 비교되어도 왼쪽 배열에 있는 요소가 우선적으로 temp 배열에 들어오게 된다. 따라서 알고리즘은 Stable로 유지되는 것을 알 수 있다.
- QuickSort è UnStable
QuickSort는 여기서 UnStable하게 측정되었다.
QuickSort는 배열 내부의 원래 요소들끼리 순회하며 값을 비교하는 것이 아니라, 임의의 pivot을 설정해 비교하는 것이기 때문에 배열의 요소 내에 Key 값 중에 동일한 것이 있느냐를 계산하지 않기 때문에 UnStable하다고 할 수 있다.
(3) 데이터 셋의 크기에 따른 알고리즘의 성능 비교
Time 시드 값을 이용해서 10억 크기의 난수 값을 생성해 random ArrayVector에 insert하였다. 그리고 random을 리턴해, 정렬을 Test하는 함수에서 사용하도록 하였다.

코드는 다음과 같이 clock() STL를 이용해 값을 받아왔고, Sort 이전과 이후의 시간 차를 계산해 출력하여 확인하였다.
이 때 InsertionSort와 SelectionSort의 경우 Quarantic-Time-Complexity인 특성을 가지고 있으므로 10만이 넘어가면 시간이 20분 이상 걸리는 것을 알 수 있었다.
그래서 if문으로 일정 이상 size가 들어오게 되면 검사를 수행하지 않는 것으로 하였다.

백 억까지 size를 늘려서 sort를 시도해보았지만 안타깝게도 MergeSort도, QuickSort도 천 만이 넘어가면 함수가 끝날 때까지 아주 오랜 시간이 걸리는 문제가 있었다.
비록 결과 화면 캡쳐는 백 억까지는 못하였지만, 천 만개의 요소를 가진 배열에서도 Sort가 정상적으로 진행됨을 알 수 있었다.
이때 하나의 genereate_random_ArrayVector() 함수가 호출되어 반환된 random 배열로 Sorting을 시도했으므로 모두 동일한 데이터셋으로, 공정하게 알고리즘의 성능을 비교하였다고 할 수 있다.
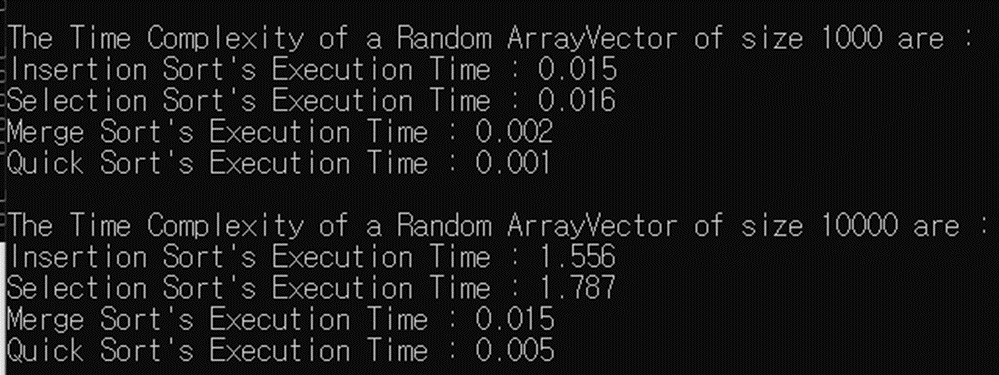
Size = 1000, Size = 10,000일 때를 대표적인 예시로 정하여 비교를 해보자. Size가 커질수록 Insertion Sort, Selection Sort와 MergeSort, QuickSort의 시간 편차는 커지고 있다.
이는 ‘시간 복잡도’라는 개념으로 설명할 수 있다.
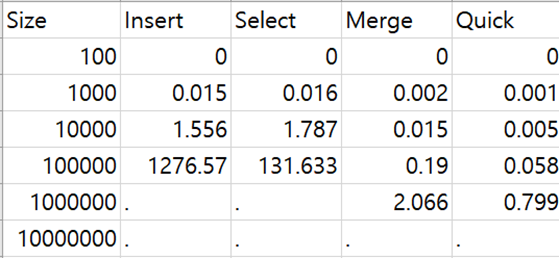
위의 표는 각 알고리즘에서 Size별로 걸리는 시간을 측정한 것이다. 이 표를 이용해서 각 알고리즘을 그래프로 그려보았다.
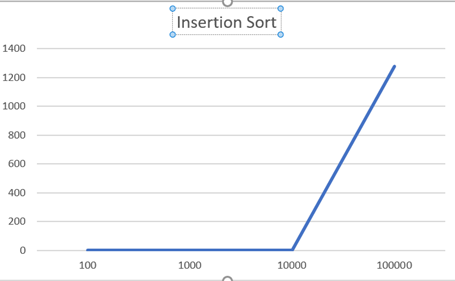
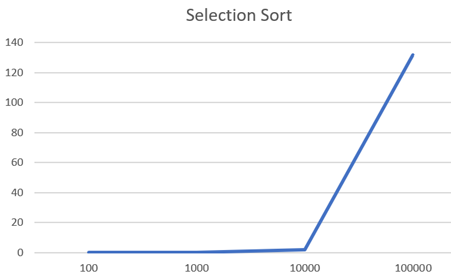
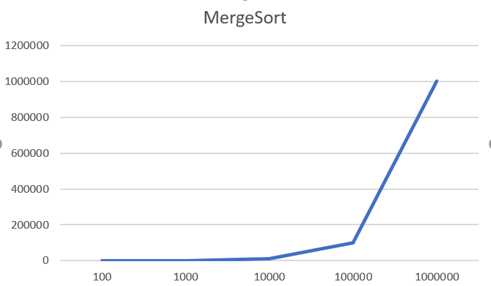
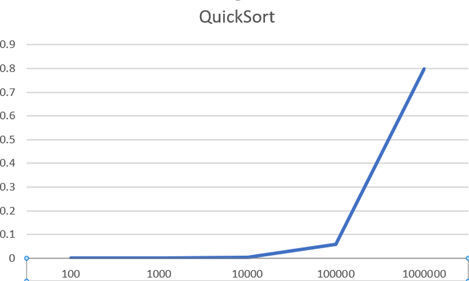
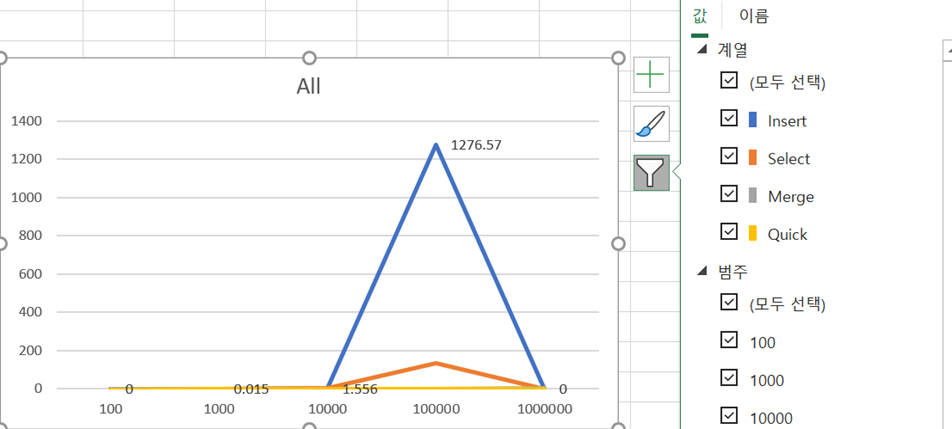
따로따로 그래프를 그려보면 모두 Size가 커질수록 시간이 크게 증가하는 것을 알 수 있는데, 한 그래프에 동일한 범주로 두고 그려보면 Inert, Select에 비해 Merge와 Quick은 훨씬 낮은 것을 볼 수 있다. (여기서 그래프가 아래로 꺾인 것은 NULL값을 그래프의 입력으로 넣어 0으로 인식한 것이다.)
여기까지 4가지 알고리즘의 성능을 비교, 분석해보았다.
3. 고찰
(1) Pair 구조체 자료형에 대한 연산자 오버로딩

Template를 사용해서 변수의 자료형을 미정한 상태로 프로그램을 짜다 보니 이런 문제가 생겼다. 정렬 내에서 ArrayVector의 멤버끼리 비교를 하는 연산자가 많이 쓰이는데, main함수에서 Pair이라는 구조체를 사용한 것에서 연산자를 어떻게 처리를 할지 모호해지는 부분이 있어 에러가 떴다. . T에 비교할 수 있는 int,double이 아닌 클래스 등이 들어왔을 때는 어떻게 비교 연산을 수행할지 모호하기 때문이다.
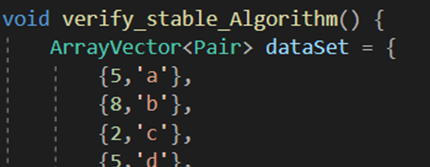
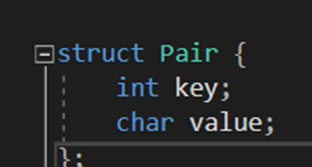
연산자 오버로딩으로 이를 해결할 수 있었고, friend를 사용해 비교 연산자, 출력 연산자를 전역에 선언해주었다.
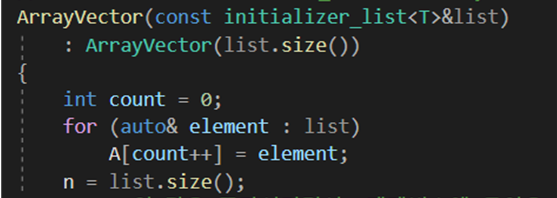
(2) Initializer_list

이렇게 중괄호를 사용해서 ArrayVector 내에 A 멤버 변수에 초기화시키는 것을 구현하고 싶어 찾아보았더니, 저렇게 중괄호로 감싸진 형태를 Initializer_list라고 한다는 것을 알았다.
ArrayVEector 클래스 내에서 복사 생성자 오버로딩으로 들어온 list의 size만큼 동적할당하고, 값을 복사해 하나의 ArrayVector 객체를 생성할 수 있었다.
'Major Study > Data Structure' 카테고리의 다른 글
| [자료구조론] Stock Span Problem 주가 스팬 구현(Linear/Quadratic-Time) (0) | 2021.11.21 |
|---|---|
| [자료구조론] C++ MergeSort (병합 정렬) 구현하기 (0) | 2021.11.21 |
| [C언어 자료구조] 검색 알고리즘/선형 검색/이진 검색 (0) | 2021.09.04 |
